흰공의 확률은?

상자 속에 공이 하나 들어 있다. 이 공은 검은색 일 수도 있고, 흰색일 수도 있다. 이 상자에 흰 공을 하나를 더 넣고 뒤흔든 다음 공을 하나 꺼냈더니 흰 공이 나왔다. 자, 상자에 남아 있는 공이 흰색일 확률은 얼마일까?

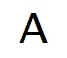
제 생각은.

이렇습니다만. 쩝. 몬테카를로가 아니라 몬티홀 문제라고 보는 것이 좋을 것 같습니다. 와하하.
* 여기에서 자루흰공 = 상자안에 흰공 이라는 뜻입니다. 흠.

Commented by highseek at 2011/04/02 17:51

인생은 반반임

Commented by 히언 at 2011/04/02 18:11

ㅎㅎ 반반한 여자가 좋긴 하죠

Commented by seha at 2011/04/02 19:57

전 트위터로 답변을 -_-;;;
그리고 흠 메모장에 남겼어요.
"히언님은 반반한 여자를 좋아한다." =3==3333

Commented by 히언 at 2011/04/02 20:21

으헉!!!

Commented by 성큼이 at 2011/04/02 21:22

처음게 흰공일 확률을 p 라고 놓으면 2/(1 + 1/p)
만약에 p가 1/2이면 2/3 이겠네용

Commented by 히언 at 2011/04/03 11:06

옷!
이 접근은 뭔지 모르겠는데 아름다운 것 같기도 하고..
설명좀 다시해 주세요.

Commented by 성큼이 at 2011/04/03 11:58

P(남은공 흰공|꺼낸공 흰공)
= P(남은공 흰공이고 꺼낸공 흰공)/P(꺼낸공 흰공)
= P(처음공 흰공)/{P(처음공흰공) + P(처음공 검은공)*P(처음공 검은공인데 꺼낸공 흰공)}
= p / {p + (1-p)*(1/2)}

이라고 계산을 했지요 ㅋㅋ 별로 아름답진 않네요 ㅋㅋ

Commented by 히언 at 2011/04/03 13:25

오! 완전 아름다운데요!

Commented by 몽몽이 at 2011/04/03 13:36

풀이해주신걸 보니 말씀이 맞는 듯

Commented by 히언 at 2011/04/03 13:32

제 생각을 달았어요. 흐흐

Commented by 몽몽이 at 2011/04/03 13:35

Sample Space가 왜 4인가요?

Commented by 히언 at 2011/04/03 13:50

제 의도는 흰공이 서로 구분이 되야 한다는 구분이고, 그랬을 때 내가 뽑을 수 있는 공의 수는 4가지 공의 경우가 있는 것이고 이때 전체 sample space는 4이고, 흰공을 뽑은 다음에 남은 구분되는 흰공의 수는 2가지라는 것이 풀이 인데요. 좀 말이 이상한가요? ㅎㅎ

Commented by 히언 at 2011/04/03 13:50

언제나 이런 문제는 많이 헷갈립니다. 으흐흐.

※ 이 포스트는 더 이상 덧글을 남길 수 없습니다.