주파수 라는 건 누가 처음에 이름을 붙였는지는 모르겠지만, 참으로 어렵게도 이름을 지었다는 느낌이 듭니다. 마치 의사들이 환자들이 알아듣지 못하는 말로 - 이 글이 의사업계에 반향을 일으키지는 않았으면 하는 바램이 있습니다만, 아니면 말고요. 휴 - 자신들만의 의사소통을 하듯이 예전에 누군가가 유식을 티 낼려고 이름을 지었을 것이라는 느낌이 들곤 합니다. 대부분의 용어가 그렇듯이, 아마도 영어나, 일본어를 우리말로 옮기는 과정에서 억지로 끼워 맞추지 않았나 싶습니다. 그래서 말인데, 이제부터는 영어 용어가 있는 경우에는 영어로 쓰는 것이 좋을 것 같은 느낌입니다. 영어용어를 남발하더라도 이해해 주세요. 감사.
- 사실은 한글로 된 책들을 읽다 보면 용어 때문에 더 힘들 때도 있더라는게 제 개인적인 의견입니다. 홀짝홀짝 읽다 보면 오히려 원서를 볼 때 보다 훨씬 이해도가 떨어져 버려 무슨 얘기를 하던 중인지 잊어 버릴 때가 있어 난감할 때도 있습니다만 -
사전에는 주파수란 진동운동에서 단위시간당 같은 것이 일어난 회수 또는 자주 일어남, 빈번, 빈도 이렇게 표현해 놓았지만, 제 나름대로의 정의는 Frequency라는 말은 "얼마나 자주?" 라는 의미이지요.
예를 들어 Cos(2πt)라는 주기 함수를 고등학교 물리 시간 때, 많이 보았죠? Cos(2πt)는 1초에 1번의 주기가 있는 함수를 말하지요. 이 함수는 일반화된 Cos(2πft)라는 함수에 주파수 f = 1 Hz을 넣고서 만들어낸 함수 인데요, Cos이라는 함수는 주파수만 알면 단방에 한줄로 표현해 낼 수 있는 아주 편리한 함수라지요. 이 함수를 예로 신호와 주파수 영역을 설명하는 것이 가장 만만할 듯 하네요
f=20kHz 일때를 예를 들어 보도록 하지요.
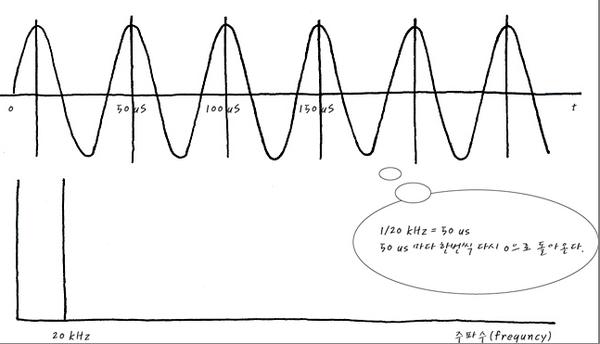
허접한 그림에서도 확인할 수 있듯이, cos(2π(20kHz)t)는 주파수 영역에서는 20KHz 하나만의 성분을 가져요.
Cos(2πt)는 시간 영역 (보통 우리가 사는 세계)에서는 구불텅한 모습으로 보입니다만, 주파수 영역에서는 한가지 주파수만 가지고 있는 것이 그 포인트 입니다. 보시다 시피, 주파수 입장에서 보면 1 Hz 하나만 있겠습니다요. 간단 그 자체네요.
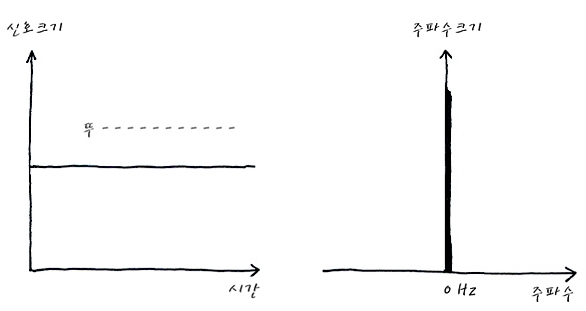
보통 Cos과 같이 주기를 갖는 신호를 AC라 하고, 주파수를 갖지 않는 주-욱 같은 크기의 레벨을 가지는 신호를 DC라고 부릅니다. 결국 주파수 = 0 Hz 인 신호를 DC라고 할 수 있겠네요. DC는 어떻게 생겼냐면요.. 심장박동이 멈췄을 때 뚜---- 하는 소리나죠. 그것처럼 쭉 이어진 신호가 DC에요. 주파수는 뚜---- 하니까, 주기가 없죠. 그러니까 0입니다요.
Fourier Transform 이라는 걸 알고 계시는지 모르겠지만, - 이제부터 알면 되니까 유쾌하게 점점 가보시지요 -
모든 신호는 무한개의 Cos 또는 Sin (주기함수)의 합으로 나타낼 수 있다가 그 요점입니다.
결국 신호를 주파수 별로 분리해 준다는 거죠.
어떤 신호 = 어떤주기의주파수성분 + 또 어떤주기의주파수성분 +또 또 어떤주기의 주파수성분 ......
이런식이고, 각각의 어떤 주기의 주파수의 정수배항들이 어떤 신호를 이루기 위하여 공헌하는 바 들이 틀린데, 그 공헌하는 바들이 각각의 크기로 나타납니다. 그 공헌하는 바를 어떤 주파수의 크기라고 할 때,
어떤 신호 = 어떤주기의주파수의 크기*어떤주기의주파수 +또 어떤주기의 주파수의 크기*또 어떤주기의 주파수 ....
이런식으로 표현할 수 있겠습니다.
예를 들어, 사각 함수는 (Rect(t))는 풀어 헤치면 무한히 많은 cos 함수의 합으로 풀어 헤칠 수 있다는 것이 Fourier Transform 입니다. 이 그림을 설명하려면, Signals & Systems 라는 과목 하나를 모두 다시 공부해야 하니까, 그건 좀 곤란하고, 이 의미에 대해서만 풀어 보도록 해야하겠습니다. - 복잡한건 딱 질색이거든요 -
Rectangular 함수는 - 이제부터 함수는 신호로 표시해도 무리는 없으리라 생각중 입니다.- Amplitude (크기 또는 높이)가 1이고, Width (길이)는 -τ/2에서부터 τ/2까지 즉 τ의 Width를 가지는 함수를 말하며, 보통 Embedded system에서의 디지털 신호는 이런 Rectangular 신호로 이루어져 있습니다. 이런 Rectuangular 신호를 주파수 영역에서 보면 주파수가 0인 부분, 즉 DC 성분이 가장 큰 portion을 차지 하며, 이 크기는 Retangular 신호의 시간 영역에서의 넓이와 같습니다. 이런 Rectangular 신호의 주파수 영역에서의 모양은 sinc function이라고 부르는 함수의 모양으로 Transform이 가능한데, - 그림의 오른쪽 주파수 영역의 그림을 보면, - 이 의미는 Rectangular 함수의 주파수 영역의DC 성분의 크기가 가장 크면서 1/τ Hz마다 (1/τ의 Harmonics)의 주파수 성분은 0이고, 나머지는 양쪽 축으로 무한히 퍼진 주파수 성분이 있음을 눈치 챌 수 있을 것입니다.
더 알기 쉬운 예로 τ = 1 인 예를 들면 재미있는 일이 벌어집니다. 1/τ = 1 이므로, 1, 2, 3, 4, 5 ... Hz 에서는 주파수 성분이 없고, Retangular 신호의 면적은 1이므로, DC성분의 크기는 1입니다.
Graph를 보는 방법은 f축은 rect(t)를 Fourier Transform하면 나오는 sinc(f)이며, 이 sinc(f) 함수의 x축은 주파수를 의미합니다. 예를 들어 보면 제일 쉽겠지요. sinc(f)의 f=1.0에서의 값은 아래 graph cose의 1Hz 성분
바로 요 성분이 없다. 즉 "0, Zero"를 의미해요. 그림에서 보면, Rectangular 함수가 시간축에서 어떤 cos함수들이 어떤 크기로 합해 져야 되는지 표현했으며, 주파수 축에서는 어떤 주파수들의 성분들이 주파수 영역에 있는지를 보여주고 있습니다.
F(f)에서 F는 Fourier Transform, f는 주파수를 의미하지요.
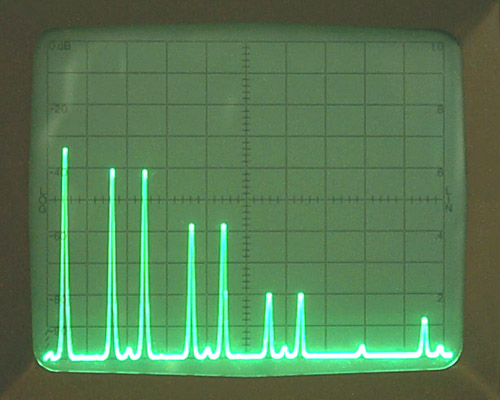
자자, 이 원리는 바로 Spectrum Analyzer라는 계측기에서 나오는 결과를 대변하게 되는데요. 어떤 디지털 신호를 Spectrum Analyzer라는 계측기에 물리면, 곧바로 주파수 영역에서 어떤 주파수 성분들로 이루어져 있는지 보여줍니다. 오, 편한세상입니다.
결국엔, 이세상의 모든 신호는 Cos과 Sin의 합으로 나타낼 수 있다가 바로 결론이며, 대충은 DC 쪽에 가까운 완전 저주파 신호와 - DC를 포함한 - AC라고 불리우는 약간의 중주파 (음..) 신호들로 표시하며, 보통 디지털 신호는 이런 rectangular function의 모양이니까, 여전히 DC + AC와 완전 필요 없는 전대역에 걸쳐 있는 자잔한 고주파 신호로 생겨먹었다고 생각하시면 됩니다.
Spctrum Analyzer 화면 사진
다음 사족에 관해서는, 굳이 이해하려고 하지 않으셔도 됩니다. 그냥 궁금한 사람을 위한 짧은 얘기인데, 굳이 이해 못해도 상관없습니다.
* 그런데 주파수 영역에서 왠 마이너스 크기의 주파수를 갖냐고 의문을 갖는다면, 그건 좀 다른 문제입니다. Fourier Transform은 ejwt라는 basis function의 합으로 나타내는데, 이 녀석이 complex이다 보니, Xcos + jYsin 으로 나타내니까, Eualer 공식에 의해 phase가 여기에 따라 붙어 마이너스 처럼 보이지만, 실제 크기를 따지고 싶으면, sinc function의 절대값을 제곱해 버리면, Power Spectral Density가 나와서 모두 +의 실제 Power 크기가 나오니, 걱정 끝입니다.
* : 이후 DC성분은 DC를 포함한 저주파 성분, AC성분은 왠만큼의 주파수를 가지고 있는 고주파 성분을 의미하겠습니다. 좀 애매모호 하지만요.
* http://www.falstad.com/fourier/ 요기에 가보시면, 주파수 성분을 만지면, 실제 신호는 어떻게 변화되는가를 관찰 할 수 있는 Java APPLet이 있어요.
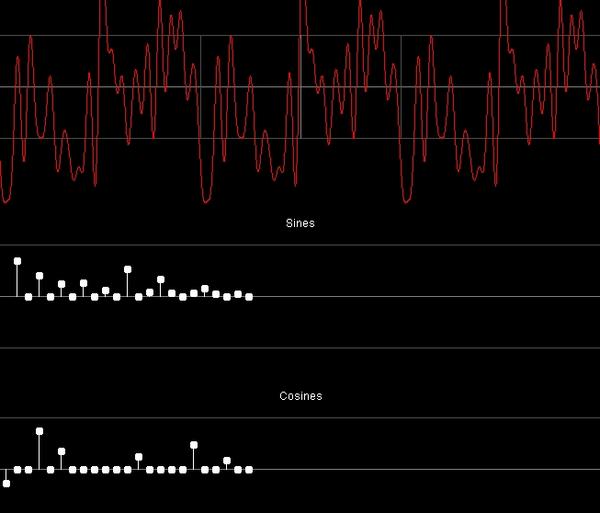
뭐 이런식인데요, 원래 4각형이 있던 신호에 sin과 cos 성분을 바꾸면 어떻게 신호가 변하는지 곧바로 보여줘요. 한번 봐보세요. 신기하다니까요.
Linked at 임베디드 시스템 개발자 되기 .. at 2009/06/12 22:58 Linked at 더러운 북극토끼님의 이글루입니.. at 2015/10/07 15:33 Linked at [임베디드 레시피] 신호와 주.. at 2018/10/09 02:58 Commented by 지섭 at 2009/07/18 11:37 
Commented by 히언 at 2009/07/20 20:45 Commented by 장상길 at 2009/07/27 13:37 
친절한 임베디드 시스템 개발자 되기 강좌 글 전체 리스트 (링크) - 
댓글